COMPTE RENDU DES SEANCES DE L'ACADEMIE DES SCIENCES
Janvier-Juin
T. XL
Nº. 22
Pag. 1157, 1158, 1159, 1160, 1161, 1162, 1163, 1164
*
PHYSIQUE. - Note sur un moyen photographique de déterminer la hauteur des nuages; par M. POUILLET
« Dans une communication que j’ai faite à l’Académie, il y a quinze ans ( Comptes rendus, t. XI, p.717, année 1840), on trouve un historique des diverses méthodes qui ont été imaginées pour déterminer la hauteur des nuages. Toutes ces méthodes, comme celles de Bernoulli, de Lambert et de M. Arago, reposent sur le principe des observations isolées, c’est-a-dire des observations faites en un seul point, par un seul observateur. Aprés avoir examiné ce principe en lui-même et dans les résultats qu’il avait produits jusque-lá, j’étais amené a cette conclusion: qu’il pouvait bien servir à résoudre la question dans quelques cas particuliers et en quelque sorte exceptionnels, mais qu’il resterait toujours impuissant à résoudre la question générale de la distribution des nuages dans les diverses régions de l’atmosphere.
« Dans une communication que j’ai faite à l’Académie, il y a quinze ans ( Comptes rendus, t. XI, p.717, année 1840), on trouve un historique des diverses méthodes qui ont été imaginées pour déterminer la hauteur des nuages. Toutes ces méthodes, comme celles de Bernoulli, de Lambert et de M. Arago, reposent sur le principe des observations isolées, c’est-a-dire des observations faites en un seul point, par un seul observateur. Aprés avoir examiné ce principe en lui-même et dans les résultats qu’il avait produits jusque-lá, j’étais amené a cette conclusion: qu’il pouvait bien servir à résoudre la question dans quelques cas particuliers et en quelque sorte exceptionnels, mais qu’il resterait toujours impuissant à résoudre la question générale de la distribution des nuages dans les diverses régions de l’atmosphere.
« En conséquence, je proposais une nouvelle méthode reposant sur le principe des observations simultanées, c’est-à-dire des observations faites simultanément par deux observateurs aux extrémités d’une base de longueur connue. Quelques expériences, que j’avais pu faire d’après ce principe, ne laissaient aucun doute dans mon esprit sur les avantages que l’on en pourrait tirer, pourvu toutefois que l’on consentît à faire les dépenses nécessaires pour l’appliquer dans les conditions les plus convenables.
« Depuis cette époque on a fait de nouvelles tentatives pour revenir au principe des observations isolées : M.Wartmann a proposé une méthode qui me paraît très-peu applicable (Annales de Chimie et de Physique, 3e série, t. XXIV, p. 208, année 1848); notre confrère, M. Bravais, à la même époque, en a proposé une autre, qu’il a du moins soumise à quelques épreuves (Annales de Chimie et de Physique, 3e série, t. XXIV, p. 497, année 1848), mais celle-ci même me semble restreinte dans des limites trop étroites.
« Ces nouveaux essais n’ont donc rien changé à mon ancienne conviction sur la nécessité d’avoir recours au principe des observations simultanées. Diverses circonstances ayant ramené mon attention sur ce sujet, je m’en suis occupé à plusieurs reprises, cherchant tantôt à mieux assurer l’action simultanée des deux observateurs, tantôt à simplifier l’établissement des moyens rapides de transport pour les rendre moins embarrassants et surtout moins dispendieux. Enfin, pour affranchir le probléme des difficultés de cette espéce, qui me semblaient toujours considérables, j’en ai cherché la solution dans les découvertes de la photographie, et je vais expliquer, en peu de mots, comment les expériences pourraient se faire par ce nouveau moyen, et comment deux appareils photographiques peuvent remplacer, avec d’incontestables avantages, les deux observateurs très-habiles qu’exigeait nécessairement le système dont il s’agit.
» Les objectifs photographiques peuvent embrasser un champ d’environ 28 degrés, et en même temps donner des images sensiblement planes de l’ensemble des objets disposés sur un plan perpendiculaire à l’axe. Ainsi, en imaginant que le centre optique d’un tel objectif soit le sommet d’un double cône dont la génératrice fasse avec l’axe un angle de 14 degrés, il arrive que chaque section perpendiculaire que l’on peut concevoir dans ce cône, à une distance convenable en avant, vient donner son image dans une section correspondante, placée en arriére; de plus, les distances du centre optique à chacune de ces deux sections se trouvent liées entre elles par la formule générale des lentilles,
1/b=1/f-1/m
« f , distance focale principale des lentilles;
« b , distance de la section où se trouve l’objet;
« m , distance de la section où se trouve l’image.
» En photographie, les valeurs qu’il est permis de donner à f dépendent de plusieurs éléments, et surtout de l’intensité de la lumière qui est nécessaire pour produire l’effet voulu sur la couche sensible. Dans la question qui nous occupe, la valeur de f pourra varier de 50 à 70 centimétres: nous adopterons comme moyenne 60 centimétres.
« Avec cette donnée il est facile de voir qne l’objet étant placé à 600 métres ou 1000 fois la distance focale principale, l’image doit se faire à une distance m = 0m,6006; c’est-à-dire seulement à de 6/10 millimétre plus loin que la distance focale
principale elle-même: ainsi tous les objets placés au delà de 600 métres feront leurs images très-sensiblement sur le même plan, à la distance de 60 centimètres derriére la lentille.
« Le tableau destiné à recevoir l’image du champ tout entier devra donc être un cercle de 30 centimètres de diamètre; car dans un cône de 28 degrés d’ouverture le diamètre d’une section perpendiculaire à l’axe est la moitié de sa distance au sommet.
» Pareillement, le diamètre absolu du champ est la moitié de la distance b à laquelle se trouve l’objet; ainsi, pour un objet placé, par exemple, à 2000 mètres, le diamètre réel du cercle qui forme le champ serait de 1000 mètres.
» Cela posé, concevons deux appareils photographiques égaux, ayant les axes de leurs lentilles ajustés dans la verticale et placés à 100 mètres l’un de l’autre. Les cônes qui limitent les champs respectifs, d’abord séparés a leur origine, commencent a se pénétrer a une certaine hauteur; cela arrive quand le rayon du champ est égal à la moitié de la distance qui sépare les appareils, par conséquent lorsqu’on est parvenu à une hauteur verticale double de cette distance ou 200 métres, pour l’intervalle de 100 métres que nous avons pris comme exemple. A partir de là, les deux cônes se pénétrant de plus en plus, l’espace qu’ils comprennent en commun dans un même plan horizontal devient ce que l’on peut appeler le champ commun, puisqu’il appartient a la fois aux deux appareils.
» Les cercles qui en se coupant déterminent le champ commun ont pour rayon le quart de la hauteur h à laquelle on s’élève; la ligne qui joint leurs centres reste toujours égale à la ligne sensiblement horizontale qui joint les centres optiques et qui mesure la distance d des deux stations, ainsi qu’a la ligne égale et parallèle qui joint les centres des deux tableaux; cette dernière peut être appelée la ligne de foi, parce qu’elle sert à repérer les images. D’après cela il est facile de voir que dans le sens de la ligne de foi la grandeur absolue du champ est exprimée par h/2=d tandis que dans le sens perpendiculaire elle est exprimée par
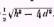 Comme il faudra d’ailleurs que le rapport de h à d soit compris entre certaines limites, on peut faire h= cd, alors les dimensions du champ commun deviennent
Comme il faudra d’ailleurs que le rapport de h à d soit compris entre certaines limites, on peut faire h= cd, alors les dimensions du champ commun deviennent
dans le sens de la ligne de foi,
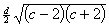 dans le sens perpendiculaire à, cette ligne; et l’on verra, pour le but qu’on se propose, qu’il est bon de faire en sorte que c ne soit ni plus petit que 10 ni plus grand que 30.
dans le sens perpendiculaire à, cette ligne; et l’on verra, pour le but qu’on se propose, qu’il est bon de faire en sorte que c ne soit ni plus petit que 10 ni plus grand que 30.« Supposons maintenant que dans toute l’étendue du champ commun le ciel soit serein, à l’exception d’un seul petit nuage de forme quelconque, dont le contour soit bien tranché, et qui se meuve dans une direction quelconque par rapport à la ligne de foi. Il est évident que l’image exacte d’un tel nuage se produira simultanément sur les tableaux des deux appareils, qu’elle y sera parfaitement reconnaissable, qu’elle occupera sur chaque tableau une place déterminée par la hauteur et la position du nuage dans le ciel, qu’elle y aura un mouvement parallèle, et que, si l’on pouvait en frapper l’empreinte au même instant sur les deux tableaux, il serait possible, à l’aspect de ces empreintes et de la place qu’elles occupent, de reconstituer la forme du nuage au sein de l’atmosphére et de déterminer la hauteur à laquelle il se trouve au-dessus du centre optique des deux appareils.
« La photographie, et la photographie seule, peut réaliser la supposition que nous venons de faire: elle peut frapper les empreintes qui sont propres à donner la hauteur du nuage, et surtout elle peut agir exactement au même instant dans les deux appareils, accomplissant cette action dans un temps assez court pour que le nuage ne lui échappe pas par la vitesse de son mouvement.
« La photographie, et la photographie seule, peut réaliser la supposition que nous venons de faire: elle peut frapper les empreintes qui sont propres à donner la hauteur du nuage, et surtout elle peut agir exactement au même instant dans les deux appareils, accomplissant cette action dans un temps assez court pour que le nuage ne lui échappe pas par la vitesse de son mouvement.
» Admettons que les glaces carrées destinées à recevoir les images portent deux lignes perpendiculaires entre elles, dont l’intersection soit prise pour le centre de la glace ou du tableau; admettons que la position de chaque glace par rapport à son objectif soit repérée, une fois pour toutes, de telle sorte que l’axe optique passe bien par son centre, et qu’en même temps l’une des perpendiculaires se trouve dans la direction de la ligne de foi. Alors les images étant reçues et fixées sur la glace, voici comment on en pourra déduire la hauteurdes nuages qu’elles représentent.
« Il est facile de voir que pour tout ce qui appartient au champ communles images sont égales, et que pour les superposer il faudrait:« 1º. Mettre en coïncidence la ligne de foi;
« 2º. Faire glisser, dans le sens de cette ligne, l’un des centres par rapport à l’autre d’une certaine quantité p que nous appellerons le déplacement.
« En effet, désignons par z1 et z2 , les points où les axes optiques du premier et du deuxième appareil vont percer le plan du champ commun où se trouve le nuage, par z3 un troisième point pris arbitrairement dans le même plan et aussi dans le champ commun; imaginons que par le centre optique du premier appareil on mène des lignes à ces trois points et qu’on les prolonge au-dessous jusqu’au plan du tableau; on formera ainsi deux pyramides semblables opposées par le sommet.
» La même construction dans le deuxiéme appareil conduira au même résultat.
« De plus, les deux grandes pyramides ayant la même base, les deux petites pyramides auront des bases égales, sous la seule condition que le premier et le deuxiéme objectif aient la même distance focale principale, comme nous l’avons supposé. Ainsi, dans ce cas, les deux images sont non seulement égales dans l’ensemble du champ, mais elles sont égales de chaque côté de la ligne de foi.
« Les deux pyramides relatives au même appareil donnent la proportion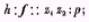 « Les deux pyramides relatives au même appareil donnent la proportionla ligne z1 z2 est égale à la distance d des centres optiques des deux objectifs; p est l’image de z1 z2: par conséquent sa valeur marque précisément de combien il faudrait faire glisser, dans le sens de la ligne de foi, le centre de la première image par rapport au centre de la deuxième, pour arriver à la coincidence des images des trois point z1, z2, z3, ou en général à la coincidence des images marquées sur les tableaux, du moins pour toute la portion du champ qui appartient à ce plan. Il en résulte
« Les deux pyramides relatives au même appareil donnent la proportionla ligne z1 z2 est égale à la distance d des centres optiques des deux objectifs; p est l’image de z1 z2: par conséquent sa valeur marque précisément de combien il faudrait faire glisser, dans le sens de la ligne de foi, le centre de la première image par rapport au centre de la deuxième, pour arriver à la coincidence des images des trois point z1, z2, z3, ou en général à la coincidence des images marquées sur les tableaux, du moins pour toute la portion du champ qui appartient à ce plan. Il en résulte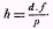 Toute la question est donc réduite à trouver la valeur de p, puisque f e d sont connus.
Toute la question est donc réduite à trouver la valeur de p, puisque f e d sont connus.
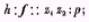 « Les deux pyramides relatives au même appareil donnent la proportionla ligne z1 z2 est égale à la distance d des centres optiques des deux objectifs; p est l’image de z1 z2: par conséquent sa valeur marque précisément de combien il faudrait faire glisser, dans le sens de la ligne de foi, le centre de la première image par rapport au centre de la deuxième, pour arriver à la coincidence des images des trois point z1, z2, z3, ou en général à la coincidence des images marquées sur les tableaux, du moins pour toute la portion du champ qui appartient à ce plan. Il en résulte
« Les deux pyramides relatives au même appareil donnent la proportionla ligne z1 z2 est égale à la distance d des centres optiques des deux objectifs; p est l’image de z1 z2: par conséquent sa valeur marque précisément de combien il faudrait faire glisser, dans le sens de la ligne de foi, le centre de la première image par rapport au centre de la deuxième, pour arriver à la coincidence des images des trois point z1, z2, z3, ou en général à la coincidence des images marquées sur les tableaux, du moins pour toute la portion du champ qui appartient à ce plan. Il en résulte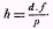 Toute la question est donc réduite à trouver la valeur de p, puisque f e d sont connus.
Toute la question est donc réduite à trouver la valeur de p, puisque f e d sont connus.» Prenons le centre de chaque glace comme origine des coordonnées et la ligne de foi comme ligne des abscisses; la partie positive étant, par exemple, à droite quand les glaces sont en place et prètes à recevoir l’action de la lumière; alors, d’aprés ce que nous venons de dire, si l’on marque sur la premiére image un point a’ et sur la deuxiéme son, point homologue a’’, de telle sorte que a’ et a” soient les deux images d’un point quelconque a du nuage, les ordonnées de a’ et a” seront égales et les abscisses différentes; de plus, cette différence des abscisses sera précisément la valeur du déplacement p.
« On pourra donc procéder de la maniére suivante: les deux glaces revètues de leurs images seront disposées sur un châssis horizontal, à la suite l’une de l’autre dans l’exacte continuation de la ligne de foi, tournées comme elles étaient quand les images se sont produites. Là elles seront éclairées en dessous par de la lumière réfléchie; alors, en regardant leur surface supérieure par transparence, on y verra, dans toute leur pureté, les images qu’elles portent; on pourra en faire la comparaison minutieuse et reconnaître tous les points homologues appartenant au champ commun. Une régle divisée reposant sur les bords du châssis pourra glisser d’une extrémité à l’autre des deux glaces en restant parallèle à elle-même et perpendiculaire à la ligne de foi; une loupe à oculaire et à fils croisés, mobile sur la longueur de cette régle, restera elle-même perpendiculaire au plan des images et pourra en parcourir toute l’étendue. On parviendra ainsi à reconnaitre successivement tous les points homologues et à mesurer avec une grande précision les différences de leurs abscisses, c’est-à-dire la valeur de p ou le déplacement qui leur appartient. Ces valeurs, substituées dans la formule, donneront les hauteurs correspondantes.
» S’il arrivait que les distances focales des objectifs fussent un peu différrentes, les deux images, au lieu d’ètre égales, seraient seulement semblables de part et d’autre de la ligne de foi; mais on pourrait encore reconnaître les points homologues a’ et a”, images du mème point a, et en déduire, par une autre proportion, la hauteur du nuage correspondant. Néanmoins il sera tonjours plus exact d’opérer avec des objectifs pareils.
« Examinons maintenant les conditions qu’il faut remplir pour que les valeurs de h sortent de la formule avec une approximation suffisante.
»1º. On peut admettre que les valeurs de h doivent être à peu près comprises entre 1000 et 15000 métres.
« 2º. On peut admettre que les appareils photographiques seront ajustés avec assez de précision pour qu’il n’y ait à craindre que de trés-petites erreurs sur la direction verticale des axes optiques, sur le repérage du centre des glaces et sur l’orientation exacte de leur ligne de foi. Ainsi, les principales erreurs porteront sur l’incertitude avec laquelle on pourra reconnaître les points homologues et déterminer la différence de leurs abscisses. Il faut donc que la valeur absolue de p ne soit pas inférieure à 20 millimétres, afin que l’erreur de 1/5 de millimètre environ que l’on pourra commettre dans sa détermination n’en soit que la centiéme partie.»
3º. Les valeurs que nous avons trouvées précédemment pour la grandeur du champ commun font voir que sa plus petite dimension est dans le sens de la ligne de foi. Or il est de la plus haute importance que cette plus petite dimension soit assez considérable pour être vue sous un angle de 20 à 25 degrés, afin que l’observateur qui la regarde et qui dirige les espé riences puisse mieux se rendre compte des limites du champ commun et de l’intervalle de temps qu’il faut aux nuages soit pour y arriver, soit pour le traverser.
« Il résulte de ces considérations que la valeur de d qui conviendra aux régions inférieures de l’atmosphère ne peut aucunement convenir aux régions supérieures; on est donc conduit a séparer les nuages en plusieurs couches et à disposer les deux appareils à des distances différentes suivant les hauteurs plus ou moins grandes vers lesquelles on voudra diriger les opérations. On pourrait, par exemple, séparer les nuages en trois couches de la manière suivante :
La première ou couche inférieure s’étendant de 1000 à 3000 mètres.
La deuxiéme ou couche moyenne s’étendant de 3000 à 9000 ´´
La troisiéme ou couche supérieure s’étendant de 9000 à 15000 ´´
Alors les distances correspondantes des deux appareils seraient:
De 100 mètres pour opérer dans la couche inférieure,
De 300 - moyenne,
De 600 - supérieure.»
Au moyen de ces dispositions, la distance focale principale étant de 60 centimètres, les valeurs de p seraient comprises entre 60 et 20 millimétres pour les deux premiers cas et entre 40 et 24 millimétres pour le troisiéme. Ainsi, dans les circonstances les plus défavorables, la hauteur des nuages serait encore donnée à moins de de sa valeur, en admettant toutefois que les erreurs d’observation ne sortent pas des limites trés-probables que j’ai indiquées plus haut.« Pour me rendre compte de la netteté des images et de la rapidité avec laquelle on peut les obtenir, j’ai eu recours à l’obligeance de l’un de nos photographes les plus habiles, M. Bertsch, qui a été des premiers à imaginer ces procédés si merveilleux au moyen desquels on obtien, en moins d’une seconde, des portraits qui ne laissent rien à désirer. M. Bertsch a bien voulu me faire quelques images d’un ciel nuageux en y employant sa méthode et ses appareils; dans un temps trés-court, qui s’éléve a peine à un quart de seconde, il a obtenu des négatifs où tous les accidents des nuages se trouvent représentés avec une fidélité parfaite. Ces essais m’ont paru décisifs; ils démontrent que, dés a présent, on peut demander a la photographie de résoudre enfin toutes les principales questions qui se rapportent à la forme, à la distribution et à la hauteur des nuages.« Les expériences peuvent être disposées de la maniére suivante: Les deux appareils sout établis à la distance jugée convenable d’aprés l’aspect des nuages; chacun a son photographe et prés de lui une cabane fixe ou portative destinée aux manipulations, car elles doivent se faire assez rapidement quand il s’agit des procédés que l’on appelle instantanés. Vers le milieu de la ligne qui sépare les appareils, s’éléve une tige verticale munie d’alidades; là, un observateur se rend compte des limites du champ commun et du moment où les nuages qu’il veut observer viendront y prendre une bonne position; quelques minutes d’avance, il fait signe aux photographes de préparer les glaces. Cela fait, il choisit l’instant favorable, d’un seul coup de manivelle il ouvre à la fois et ferme à la fois les deux appareils: la lumiére a produit son effet, les glaces ont reçu leur impression, les images sont faites; il reste seulement à les fixer par les méthodes ordinaires. Enfin, elles peuvent à loisir être portées et étudiées dans le châssis de comparaison.» Tout ce qui précède se rapporte à des observations qui seraient faites seulement dans le voisinage du zénith ; si l’on voulait les étendre à toutes les portions du ciel, les appareils deviendraient plus compliqués à cause des expériences qu’il y aurait à faire pour assurer et vérifier le parallélisme des axes optiques. »
Sem comentários:
Enviar um comentário